Foam can be defined as a two-phase system in which a gas phase is dispersed (as gas bubbles) in a liquid phase (Fig.1). The gas bubbles are separated by thin liquid films called lamellae. Foams are used to divert fluids from high permeability zones to low permeability zones during enhanced oil recovery and subsurface remediation of contaminated soils. Foam mobility in porous media is governed by bubble texture, foam trapping, bubble generation, and bubble coalescence. Published reports showed that foam mobility is dominated by foam trapping in the transient flow regime or low capillary pressures (Pc), while bubble coalescence dominates foam flow in the steady state regime or higher Pc. An efficient foam model is expected to capture these pore scale phenomena. However, most of the available models do not adequately account for foam trapping behaviour because their model parameters are usually determined from coreflood experiments at steady state flow regimes. Hence, they are unsuitable for simulating transient foam flow behaviour. Some mechanistic population balance models incorporate the effect of foam trapping on gas mobility through the relative permeability (Kr) function, such that the Kr of the flowing foam is a function of only the flowing foam saturation. However, a constitutive equation is required to predict the flowing foam fraction. Some of the variables in this equation are also obtained from experimental data at steady state, while experimental methods to measure other variables remain elusive and challenging.
The bubble population balance mechanistic model by Kovscek and Radke (1993) incorporated the effect of foam trapping on gas mobility through the relative permeability function. The model partitions foam flow into three phases namely, the aqueous phase flowing in the smallest pores, the trapped foam in the intermediate pores, and the flowing foam in the largest pores. The model then adopts the “Stone type” relative permeability model such that the relative permeability of the flowing foam is a function of only the flowing foam saturation. A constitutive equation (equation (1) in Table 1) is required to predict the fraction of the mobile foam.
The trapped foam fraction (Xt) in the equation is a function of the maximum trapped foam fraction (Xt,max), number of gas bubbles in the trapped foam (nt), and a trapping parameter (β). However, the maximum trapped foam fraction can be obtained from experimental data at steady state, while other parameters, such as number of trapped gas bubbles (nt) and trapping parameters (β) are not as straightforward. At CPG, a mechanistic experimental method is being investigated that allows values of trapped and flowing foam fraction to be measured directly at different capillary pressures and water saturation during foam flow in a consolidated porous medium. With this approach, the population balance model can be implemented to obtain a continuous relative permeability curves for both foam and water during transient and steady state flow, without the need to indirectly infer nt and β. Furthermore, a continuous capillary pressure curve can be generated for foam flow.
To achieve this method, a novel coreflood procedure was adopted that allows flowing foam fraction to be measured directly at different Pc and water saturations during foam flow. In this approach, a consolidated porous medium is treated like a bundle of capillaries of various sizes. The method relies on in-situ saturation monitoring tools (such as electrical resistivity, X-ray, NMR, MRI, CT scan) coupled with high-resolution pressure transducer during core flooding process (Fig. 2). Multiple cycles of foam alternating surfactant solutions are implemented to generate a data array of trapped and flowing foam as a function of water saturations and capillary pressures (Fig. 3). With this, an Initial-residual (IR)-curves were generated for foam transport (Fig. 4). Also, graphical analysis (Fig. 3) of the generated dataset yields multiple foam parameters (Table 1) namely: foam trapping coefficient, flow rate of mobile foam, limiting capillary pressure, critical water saturation below which foam ruptures, minimum pressure drop to propagate foam across a porous media, gas mobility reduction factor, and relative permeability curves for foam, gas, and water – all from a single coreflood experiment.
The IR and Kr curves (Fig. 4 and 5) exhibit behaviours that are consistent with established physics of foam flow in porous media. The measured Pc curves also compared reasonably with porous plate Pc measurements, which thus validates the accuracy of the methodology in treating a consolidated porous medium as a bundle of capillaries. The measured foam limiting capillary pressure (Pc*) values also showed a good trend with those reported in the literature. The method has a potential for generating multiple impute data for mechanistic foam modelling.
CPG is currently developing more facilities and resources to advance this research area. The overall objectives of this research effort are to aid fundamental understanding of foam transport, create new understanding of foam transport, and ultimately provide accurate measurements of foam model parameters for reservoir simulation of foam transport in porous media. The current research team at CIPR includes Dr. Abdulrauf Adebayo, Dr. Mazen Kanj, Dr. Sivabalan Sakthivel, and Mr. Rahul Salin.
![Figure 1. Foam bubbles analysed using both optical and confocal laser scanning microscopy [Ref.1]. Figure 1. Foam bubbles analysed using both optical and confocal laser scanning microscopy [Ref.1].](https://cpg.kfupm.edu.sa/wp-content/uploads/2020/05/CPG-Knowledge-Dr.-Rauf.jpg)
Figure 1. Foam bubbles analysed using both optical and confocal laser scanning microscopy [Ref.1].
![Figure 2. Coreflooding set up equipped with ISSM tool (Resistivity) and high-resolution digital differential-pressure transducers [Ref. 2]. Figure 2. Coreflooding set up equipped with ISSM tool (Resistivity) and high-resolution digital differential-pressure transducers [Ref. 2].](https://cpg.kfupm.edu.sa/wp-content/uploads/2020/05/Fig-2-Dr.-Rauf.jpg)
Figure 2. Coreflooding set up equipped with ISSM tool (Resistivity) and high-resolution digital differential-pressure transducers [Ref. 2].
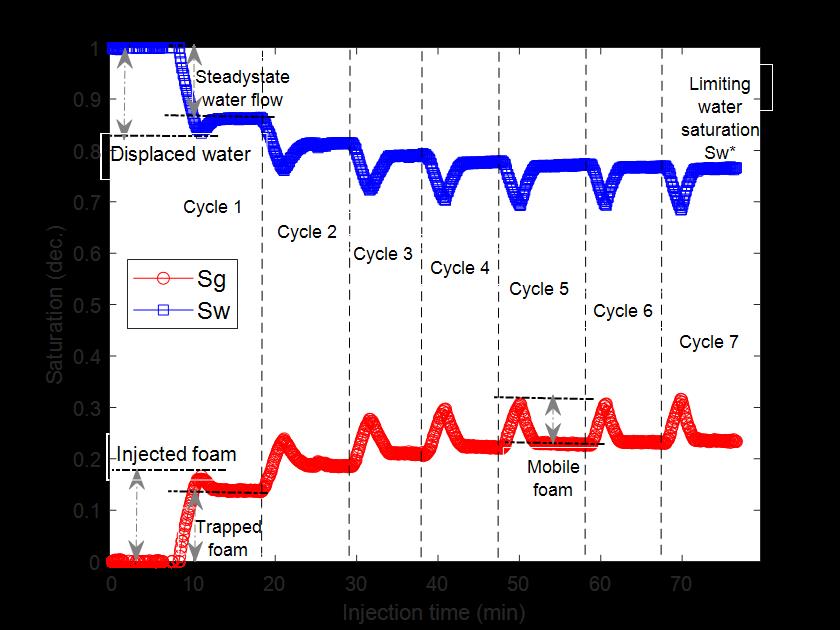
Figure 3 - Real time measurements of in-situ saturation during coreflooding.
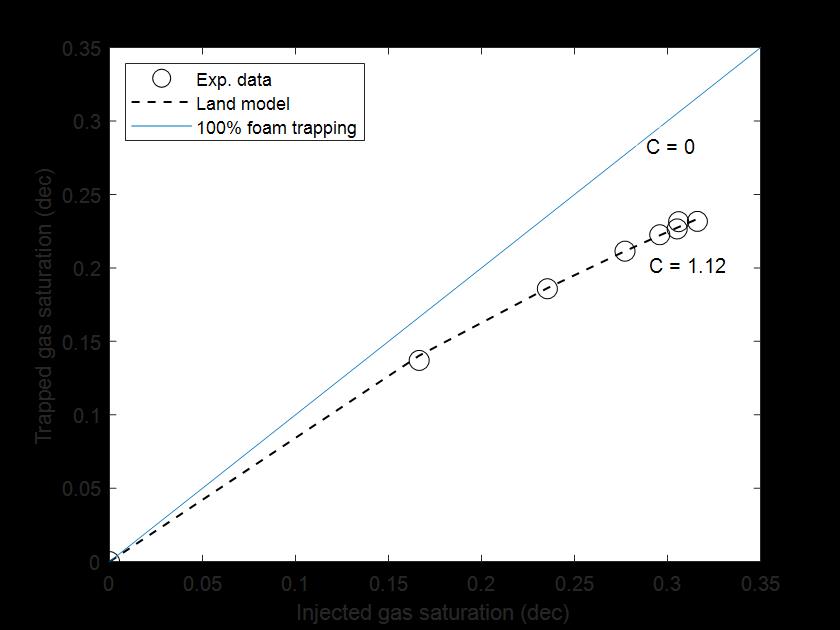
Figure 4. Relationship between cumulative trapped foam and cumulative gas injection. Also shown is the foam trapping coefficient based on Land (1968) model.
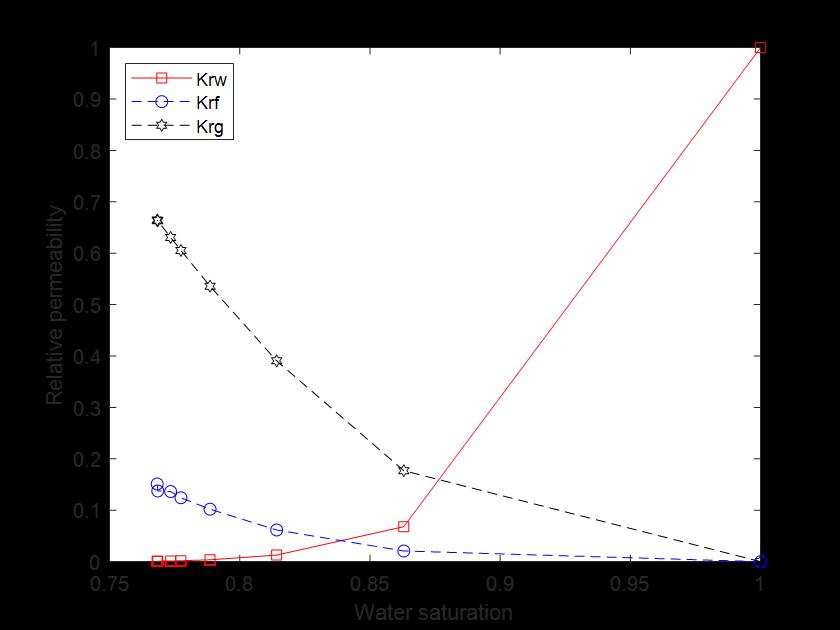
Figure 5- Relative permeability curves for water, gas (with foam), gas (without foam).
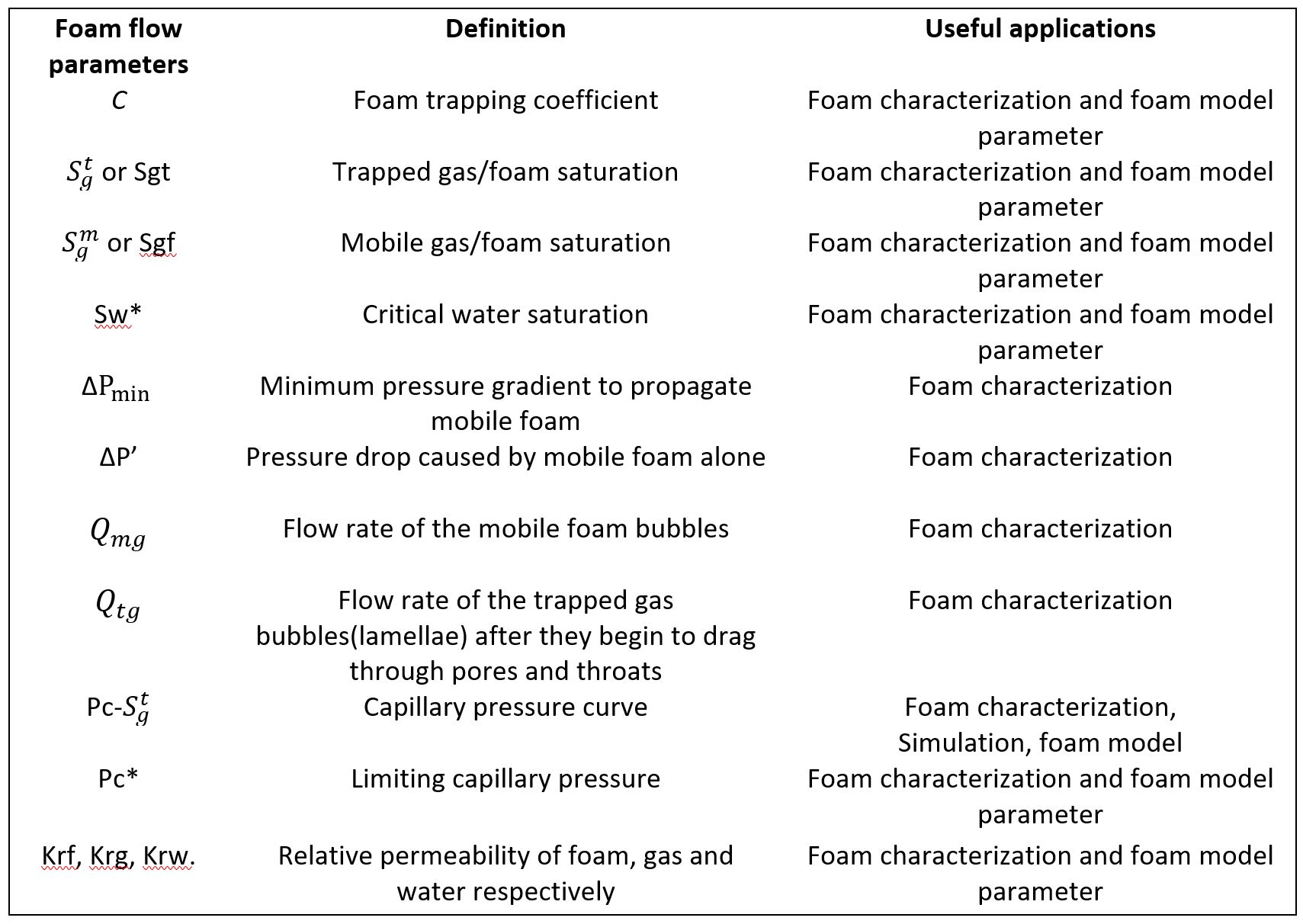
Table 1. Summary of foam flow parameters that can be derived from this method (Ref. 2 – 4).
![Equations [Ref. 2 – 6]. Equations [Ref. 2 – 6].](https://cpg.kfupm.edu.sa/wp-content/uploads/2020/05/Equation-Dr.-Rauf.jpg)
Equations [Ref. 2 – 6].
The team at CPG includes include Dr Abdulrauf Adebayo, Dr Mazen Kanj, Dr Sivabalan Sakthivel, and Mr. Rahul Salin.
References
- Sivabalan Sakthivel, Abdulrauf Adebayo, Mazen Yousef Kanj. Experimental Evaluation of Carbon Dots Stabilized Foam for Enhanced Oil Recovery. Energy Fuels 2019, 33, 10, 9629-9643. September 4, 2019. https://doi.org/10.1021/acs.energyfuels.9b02235
- Abdulrauf Rasheed Adebayo, Mazen Y. Kanj, Exploring a mechanistic approach for characterizing transient and steady state foam flow in porous media, Journal of Natural Gas Science and Engineering, Volume 60, 2018, Pages 214-227, ISSN 1875-5100, https://doi.org/10.1016/j.jngse.2018.10.016.
- Abdulrauf Rasheed Adebayo, Measurements of capillary pressure and relative permeability curves for foam transport in porous media-A capillary bundle approach, Journal of Petroleum Science and Engineering, Volume 172, 2019, Pages 1048-1056, ISSN 0920-4105, https://doi.org/10.1016/j.petrol.2018.09.012.
- Abdulrauf Rasheed Adebayo, Viability of foam to enhance capillary trapping of CO2 in saline aquifers—An experimental investigation, International Journal of Greenhouse Gas Control, Volume 78,2018, Pages 117-124, ISSN 1750-5836, https://doi.org/10.1016/j.ijggc.2018.08.003
- Kovscek, A.R., Patzek, T.W., and Radke, C. J. A mechanistic population balance model for transient and steady-state foam flow in Boise sandstone. Chemical Engineering Science, 50 (23), 3783-3799 (1995). https://doi.org/10.1016/0009-2509(95)00199-F
- Land, C.S. Calculation of Imbibition Relative Permeability for Two- and Three-Phase Flow from Rock Properties. SPE J. 8 (2): 149–156 (1968). SPE-1942-PA. http://dx.doi.org/10.2118/1942-PA
